Shape-Constrained Regression using Sum of Squares Polynomials
Under review @ Operations Research Journal, 2020
Mihaela Curmei, Georgina Hall. https://arxiv.org/abs/2004.03853
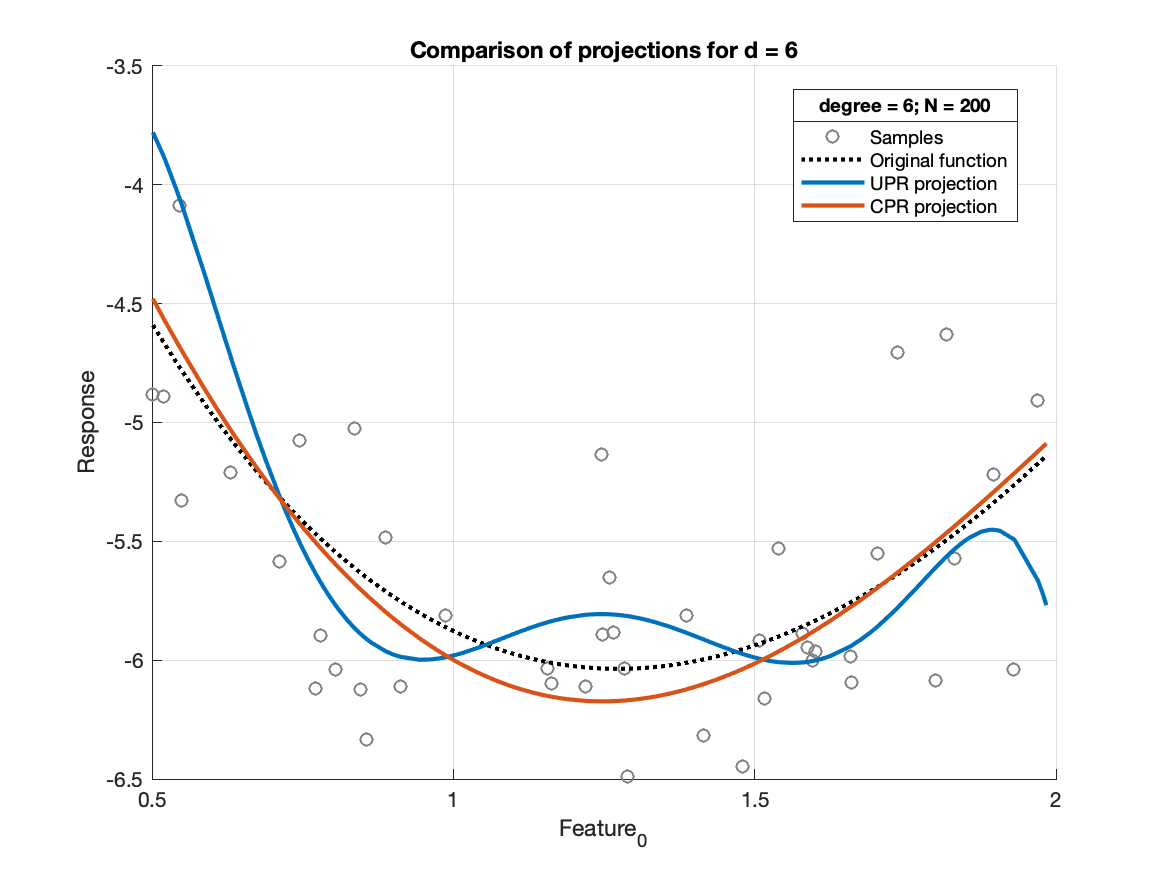
The goal of this paper is to study the problem of multivariate shape-constrained polynomial regression, which is the problem of fitting a multivariate polynomial regressor to datapoints with constraints on the shape of the regressor. We focus on two types of shape constraints here: convexity constraints and bounded-derivative constraints, with both of these shape constraints being required to hold only over a box, rather than globally. Constraints of this type appear quite frequently in a number of areas including economics, operations research, and pricing. We show how to use semidefinite programming to obtain polynomial regressors that have these properties. We further show that, under some assumptions on the generation of the data points, the regressors obtained are consistent estimators of the underlying shape-constrained function that maps the feature vectors to the responses.